Getting started with mverse

Source: vignettes/mverse_gettingstarted.Rmd

Simple Example: Transform and Summarise One Numeric Column

Suppose that we have a column col1 that we wish to transform in three different ways and compute the five number summary of the column after the transformations.

library(mverse)
## Loading required package: multiverse
## Loading required package: knitr
## 
## Attaching package: 'mverse'
## The following object is masked from 'package:multiverse':
## 
##     execute_multiverse
## The following objects are masked from 'package:stats':
## 
##     AIC, BIC
library(tibble)
library(dplyr)
## 
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union
library(ggplot2)
set.seed(6)
df <- tibble(col1 = rnorm(5, 0, 1), col2 = col1 + runif(5))

Step 1: create_multiverse of the data frame

Step 2: mutate_branch to transform col1 

# Step 2: create a branch - each branch corresponds to a universe

transformation_branch <- mutate_branch(col1 = col1,
                                       col1_t1 = log(abs(col1 + 1)),
                                       col1_t2 = abs(col1))

Step 3: add_mutate_branch to mv 

mv <- mv |> add_mutate_branch(transformation_branch)

Step 4: execute_multiverse to execute the transformations

Step 5: Extract Transformed Values from mv

extract to add the column to df_transformed that labels transformations.

df_transformed <- extract(mv)

df_transformed |> head()
## # A tibble: 6 × 3
##   universe transformation_branch transformation_branch_branch
##   <fct>                    <dbl> <fct>                       
## 1 1                       0.270  col1                        
## 2 1                      -0.630  col1                        
## 3 1                       0.869  col1                        
## 4 1                       1.73   col1                        
## 5 1                       0.0242 col1                        
## 6 2                       0.239  col1_t1

Step 5: use tidyverse to compute the summary and plot the distribution of each transformation (universe) 

df_transformed |>
  group_by(transformation_branch_branch) |>
  summarise(n = n(),
            mean = mean(transformation_branch),
            sd = sd(transformation_branch),
            median = median(transformation_branch),
            IQR = IQR(transformation_branch))
## # A tibble: 3 × 6
##   transformation_branch_branch     n  mean    sd median   IQR
##   <fct>                        <int> <dbl> <dbl>  <dbl> <dbl>
## 1 col1                             5 0.452 0.893  0.270 0.844
## 2 col1_t1                          5 0.179 0.755  0.239 0.601
## 3 col1_t2                          5 0.704 0.658  0.630 0.599

df_transformed |>
  ggplot(aes(x = transformation_branch)) + geom_histogram(bins = 3) +
  facet_wrap(vars(transformation_branch_branch))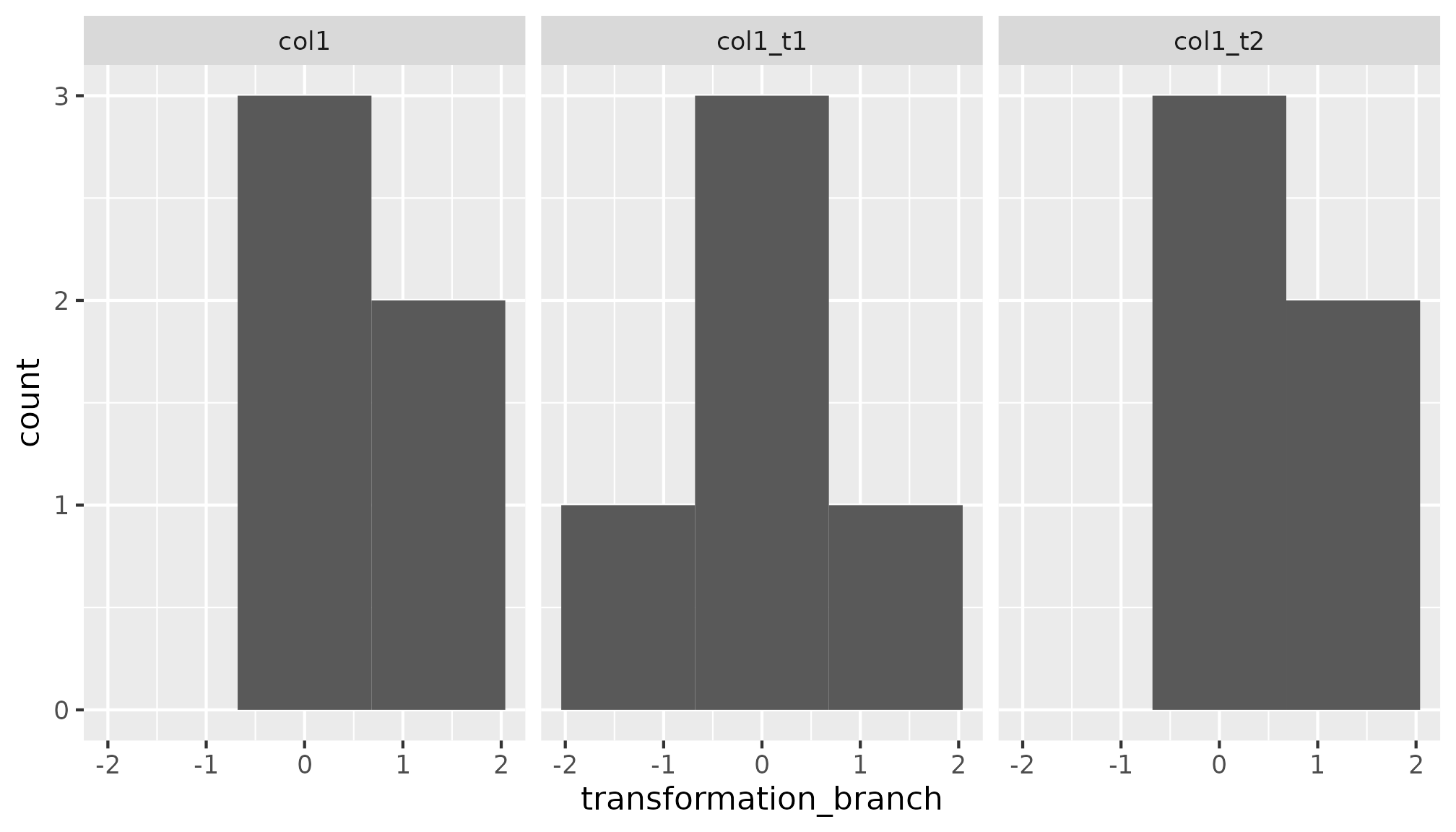

Simple Example: Using mverse to Fit Three Simple Linear Regression of a Transformed Column

Step 1: create_multiverse of the data frame

Step 2: Create formula_branch of the linear regression models 

formulas <- formula_branch(col2 ~ col1,
                           col2 ~ log(abs(col1 + 1)),
                           col2 ~ abs(col1))

Step 3: add_formula_branch to multiverse of data frame 

mv1 <- mv1 |> add_formula_branch(formulas)

Step 3: lm_mverse to compute linear regression models across the multiverse

Step 4: Use summary to extract regression output 

summary(mv1)
## # A tibble: 6 × 10
##   universe formulas_branch term    estimate std.error statistic p.value conf.low
##   <fct>    <fct>           <chr>      <dbl>     <dbl>     <dbl>   <dbl>    <dbl>
## 1 1        formulas_1      (Inter…    0.689     0.109      6.31 0.00803   0.342 
## 2 1        formulas_1      col1       0.680     0.119      5.71 0.0106    0.301 
## 3 2        formulas_2      (Inter…    0.863     0.159      5.43 0.0122    0.358 
## 4 2        formulas_2      log(ab…    0.741     0.227      3.26 0.0471    0.0178
## 5 3        formulas_3      (Inter…    0.479     0.330      1.45 0.243    -0.573 
## 6 3        formulas_3      abs(co…    0.734     0.360      2.04 0.134    -0.412 
## # ℹ 2 more variables: conf.high <dbl>, formulas_branch_code <fct>

Let’s compare using mverse to using tidyverse and base R to fit the three models.

One way to do this using tidyverse is to create a list of the model formulas then map the list to lm.

mod1 <- formula(col2 ~ col1)

mod2 <- formula(col2 ~ log(abs(col1 + 1)))

mod3 <- formula(col2 ~ abs(col1))

models <- list(mod1, mod2, mod3)

models |>
  purrr::map(lm, data = df) |>
  purrr::map(broom::tidy) |>
  bind_rows()
## # A tibble: 6 × 5
##   term               estimate std.error statistic p.value
##   <chr>                 <dbl>     <dbl>     <dbl>   <dbl>
## 1 (Intercept)           0.689     0.109      6.31 0.00803
## 2 col1                  0.680     0.119      5.71 0.0106 
## 3 (Intercept)           0.863     0.159      5.43 0.0122 
## 4 log(abs(col1 + 1))    0.741     0.227      3.26 0.0471 
## 5 (Intercept)           0.479     0.330      1.45 0.243  
## 6 abs(col1)             0.734     0.360      2.04 0.134

Using base R we can use lappy instead of

modfit <- lapply(models, function(x) lm(x, data = df))

lapply(modfit, function(x) summary(x)[4])
## [[1]]
## [[1]]$coefficients
##              Estimate Std. Error  t value    Pr(>|t|)
## (Intercept) 0.6888352  0.1090963 6.314013 0.008029051
## col1        0.6795288  0.1189216 5.714092 0.010634165
## 
## 
## [[2]]
## [[2]]$coefficients
##                     Estimate Std. Error  t value   Pr(>|t|)
## (Intercept)        0.8630266  0.1588415 5.433258 0.01223797
## log(abs(col1 + 1)) 0.7409497  0.2272193 3.260945 0.04709792
## 
## 
## [[3]]
## [[3]]$coefficients
##              Estimate Std. Error  t value  Pr(>|t|)
## (Intercept) 0.4789365  0.3303897 1.449611 0.2430335
## abs(col1)   0.7344512  0.3601450 2.039321 0.1341343

Are Soccer Referees Biased?

In this example, we use a real dataset that demonstrates how mverse makes it easy to define multiple definitions for a column and compare the results of the different definitions. We combine soccer player skin colour ratings by two independent raters (rater1 and rater2) from soccer dataset included in mverse.

The data comes from Silberzahn et al. (2014) and contains 146,028 rows of player-referee pairs. For each player, two independent raters coded their skin tones on a 5-point scale ranging from very light skin (0.0) to very dark skin (1.0). For the purpose of demonstration, we only use a unique record per player and consider only those with both ratings.

library(mverse)
soccer_bias <- soccer[!is.na(soccer$rater1) & !is.na(soccer$rater2),
                      c("playerShort", "rater1", "rater2")]
soccer_bias <- unique(soccer_bias)
head(soccer_bias)
##          playerShort rater1 rater2
## 1      lucas-wilchez   0.25   0.50
## 2         john-utaka   0.75   0.75
## 6       aaron-hughes   0.25   0.00
## 7 aleksandar-kolarov   0.00   0.25
## 8   alexander-tettey   1.00   1.00
## 9  anders-lindegaard   0.25   0.25

We would like to study the distribution of the player skin tones but the two independent rating do not always match. To combine the two ratings, we may choose to consider the following options:

  1. the mean numeric value
  2. the darker rating of the two
  3. the lighter rating of the two
  4. the first rating only
  5. the second rating only

Analysis using Base R and Tidyverse

Let’s first consider how you might study the five options using R without mverse. First, we define the five options as separate variables in R.

skin_option_1 <- (soccer_bias$rater1 + soccer_bias$rater2) / 2
skin_option_2 <- ifelse(soccer_bias$rater1 > soccer_bias$rater2,
                        soccer_bias$rater1,
                        soccer_bias$rater2)
skin_option_3 <- ifelse(soccer_bias$rater1 < soccer_bias$rater2,
                        soccer_bias$rater1,
                        soccer_bias$rater2)
skin_option_4 <- soccer_bias$rater1
skin_option_5 <- soccer_bias$rater2

We can plot a histogram to study the distribution of the resulting skin tone value for each option. Below is the histogram for the first option (skin_option_1).

library(ggplot2)
ggplot(mapping = aes(x = skin_option_1)) +
  geom_histogram(breaks = seq(0, 1, 0.2),
                 colour = "white") +
  labs(title = "Histogram of player skin tones (Option 1: Mean).",
       x = "Skin Tone", y = "Count")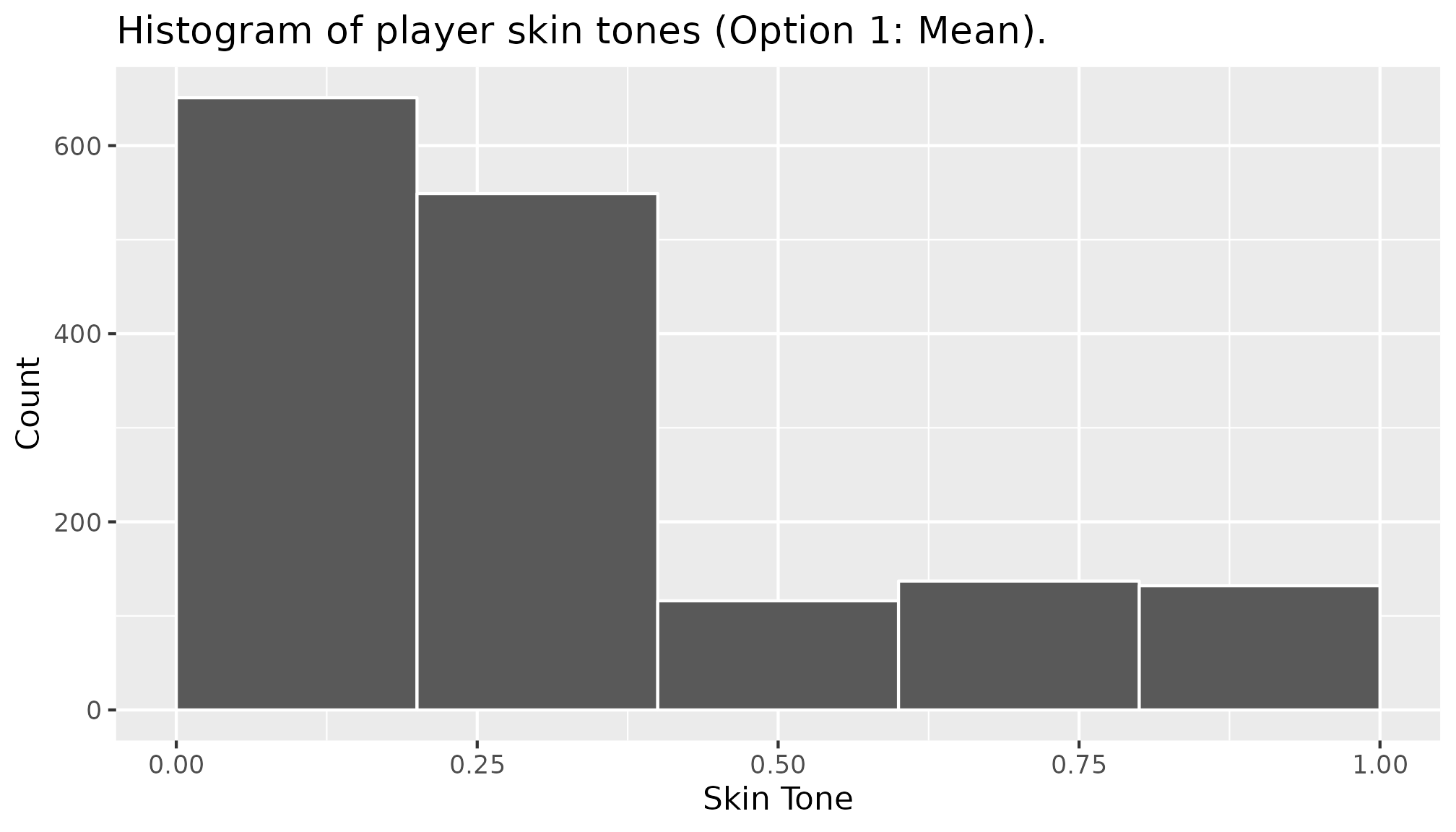

For the remaining four options, we can repeat the step above to examine the distributions, or create a new data frame combining all five options to use in a ggplot as shown below. In both cases, users need to take care of plotting all five manually.

skin_option_all <- data.frame(
  x = c(skin_option_1,
        skin_option_2,
        skin_option_3,
        skin_option_4,
        skin_option_5),
  Option = rep(
    c("Option 1: Mean",
      "Option 2: Max",
      "Option 3: Min",
      "Option 4: Rater 1",
      "Option 5: Rater 2"),
    each = nrow(df)
  )
)
ggplot(data = skin_option_all) +
  geom_histogram(aes(x = x), binwidth = 0.1) +
  labs(title = "Histogram of player skin tones for each option.",
       x = "Skin Tone", y = "Count") +
  facet_wrap(. ~ Option)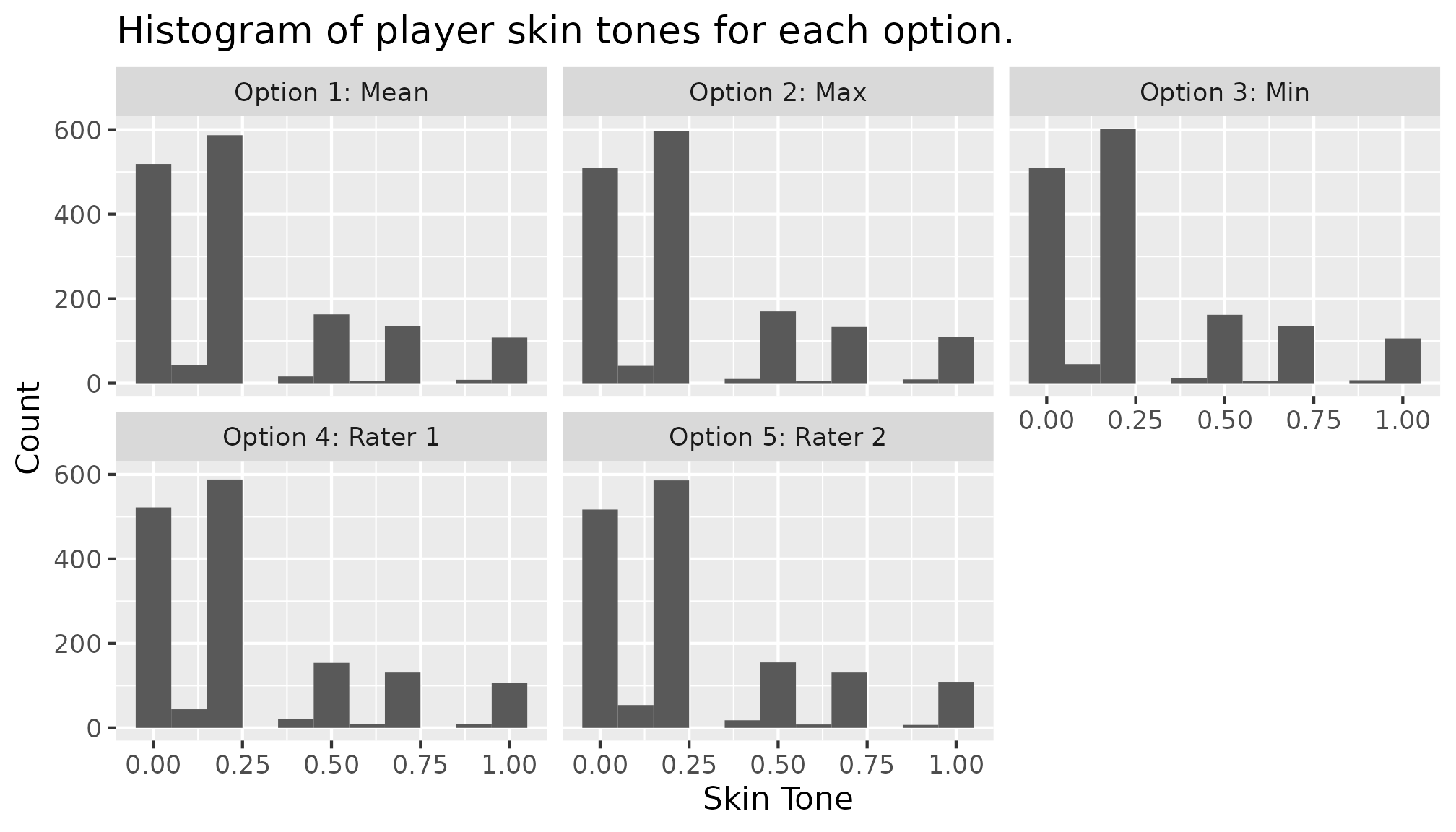

Analysis Using mverse

Branching Using mverse

We now turn to mverse to create the five options above. First, we define an mverse object with the dataset. Note that mverse assumes a single dataset for each multiverse analysis.

soccer_bias_mv <- create_multiverse(soccer_bias)

A branch in mverse refers to different modelling or data wrangling decisions. For example, a mutate branch - analogous to mutate method in tidyverse’s data manipulation grammar, lets you define a set of options for defining a new column in your dataset.

You can create a mutate branch with mutate_branch(). The syntax for defining the options inside mutate_branch() follows the tidyverse’s grammar as well.

skin_tone <- mutate_branch(
  (rater1 + rater2) / 2,
  ifelse(rater1 > rater2, rater1, rater2),
  ifelse(rater1 < rater2, rater1, rater2),
  rater1,
  rater2
)

Then add the newly defined mutate branch to the mv object using add_mutate_branch().

soccer_bias_mv <- soccer_bias_mv |> add_mutate_branch(skin_tone)

Adding a branch to a mverse object multiplies the number of environments defined inside the object so that the environments capture all unique analysis paths. Without any branches, a mverse object has a single environment. We call these environments universes. For example, adding the skin_tone mutate branch to mv results in \(1 \times 5 = 5\) universes inside mv. In each universe, the analysis dataset now has a new column named skin_tone - the name of the mutate branch object.

You can check that the mutate branch was added with summary() method for the mv object. The method prints a multiverse table that lists all universes with branches as columns and corresponding options as values defined in the mv object.

summary(soccer_bias_mv)
## # A tibble: 5 × 3
##   universe skin_tone_branch skin_tone_branch_code                  
##   <fct>    <fct>            <fct>                                  
## 1 1        skin_tone_1      (rater1 + rater2)/2                    
## 2 2        skin_tone_2      ifelse(rater1 > rater2, rater1, rater2)
## 3 3        skin_tone_3      ifelse(rater1 < rater2, rater1, rater2)
## 4 4        skin_tone_4      rater1                                 
## 5 5        skin_tone_5      rater2

At this point, the values of the new column skin_tone are only populated in the first universe. To populate the values for all universes, we call execute_multiverse.

execute_multiverse(soccer_bias_mv)

Summarizing The Distribution Of Each Branch Option

In this section, we now examine and compare the distributions of skin_tone values between different options. You can extract the values in each universe using extract(). By default, the method returns all columns created by a mutate branch across all universes. In this example, we only have one column - skin_tone.

branched <- mverse::extract(soccer_bias_mv)

branched is a dataset with skin_tone values. If we want to extract the skin_tone values that were computed using the average of the two raters then we can filter branched by skin_tone_branch values equal to (rater1 + rater2) / 2. Alternatively, we could filter by universe == 1.

branched |>
  filter(skin_tone_branch == "(rater1 + rater2) / 2") |>
  head()
## [1] universe         skin_tone        skin_tone_branch
## <0 rows> (or 0-length row.names)

The distribution of each method for calculating skin tone can be computed by grouping the levels of skin_tone_branch.

branched |>
  group_by(skin_tone_branch) |>
  summarise(n = n(),
            mean = mean(skin_tone),
            sd = sd(skin_tone),
            median = median(skin_tone),
            IQR = IQR(skin_tone))
## # A tibble: 5 × 6
##   skin_tone_branch     n  mean    sd median   IQR
##   <fct>            <int> <dbl> <dbl>  <dbl> <dbl>
## 1 skin_tone_1       1585 0.290 0.291   0.25 0.375
## 2 skin_tone_2       1585 0.320 0.297   0.25 0.5  
## 3 skin_tone_3       1585 0.259 0.295   0.25 0.25 
## 4 skin_tone_4       1585 0.269 0.297   0.25 0.5  
## 5 skin_tone_5       1585 0.310 0.297   0.25 0.5

Selecting a random subset of rows data is useful when the multiverse is large. The frow parameter in extract() provides the option to extract a random subset of rows in each universe. It takes a value between 0 and 1 that represent the fraction of values to extract from each universe. For example, setting frow = 0.05 returns approximately 5% of values from each universe (i.e., skin_tone_branch in this case).

frac <- extract(soccer_bias_mv, frow =  0.05)

So, each universe is a 20% of the random sample.

frac |>
  group_by(universe) |>
  tally() |>
  mutate(percent = (n / sum(n)) * 100)
## # A tibble: 5 × 3
##   universe     n percent
##   <fct>    <int>   <dbl>
## 1 1           79      20
## 2 2           79      20
## 3 3           79      20
## 4 4           79      20
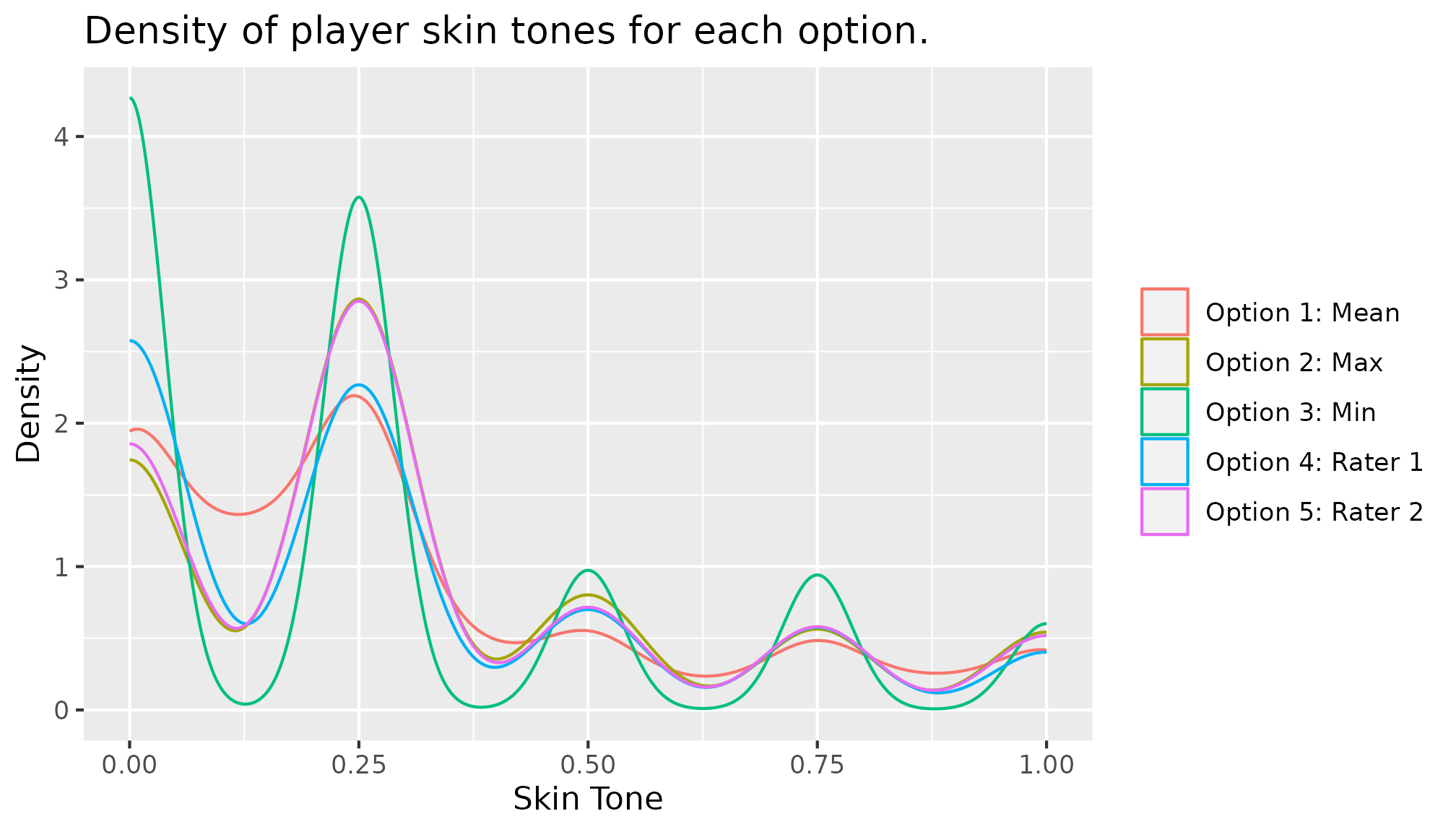
## 5 5           79      20

Finally, we can construct plots to compare the distributions of skin_tone in different universes. For example, you can overlay density lines on a single plot.

branched |>
  ggplot(mapping = aes(x = skin_tone, color = universe)) +
  geom_density(alpha = 0.2) +
  labs(title = "Density of player skin tones for each option.",
       x = "Skin Tone", y = "Density") +
  scale_color_discrete(
    labels = c("Option 1: Mean",
               "Option 2: Max",
               "Option 3: Min",
               "Option 4: Rater 1",
               "Option 5: Rater 2"),
    name = NULL
  )

Another option is the use ggplot’s facet_grid function to generate multiple plots in a grid. facet_wrap(. ~ universe) generates individual plots for each universe.

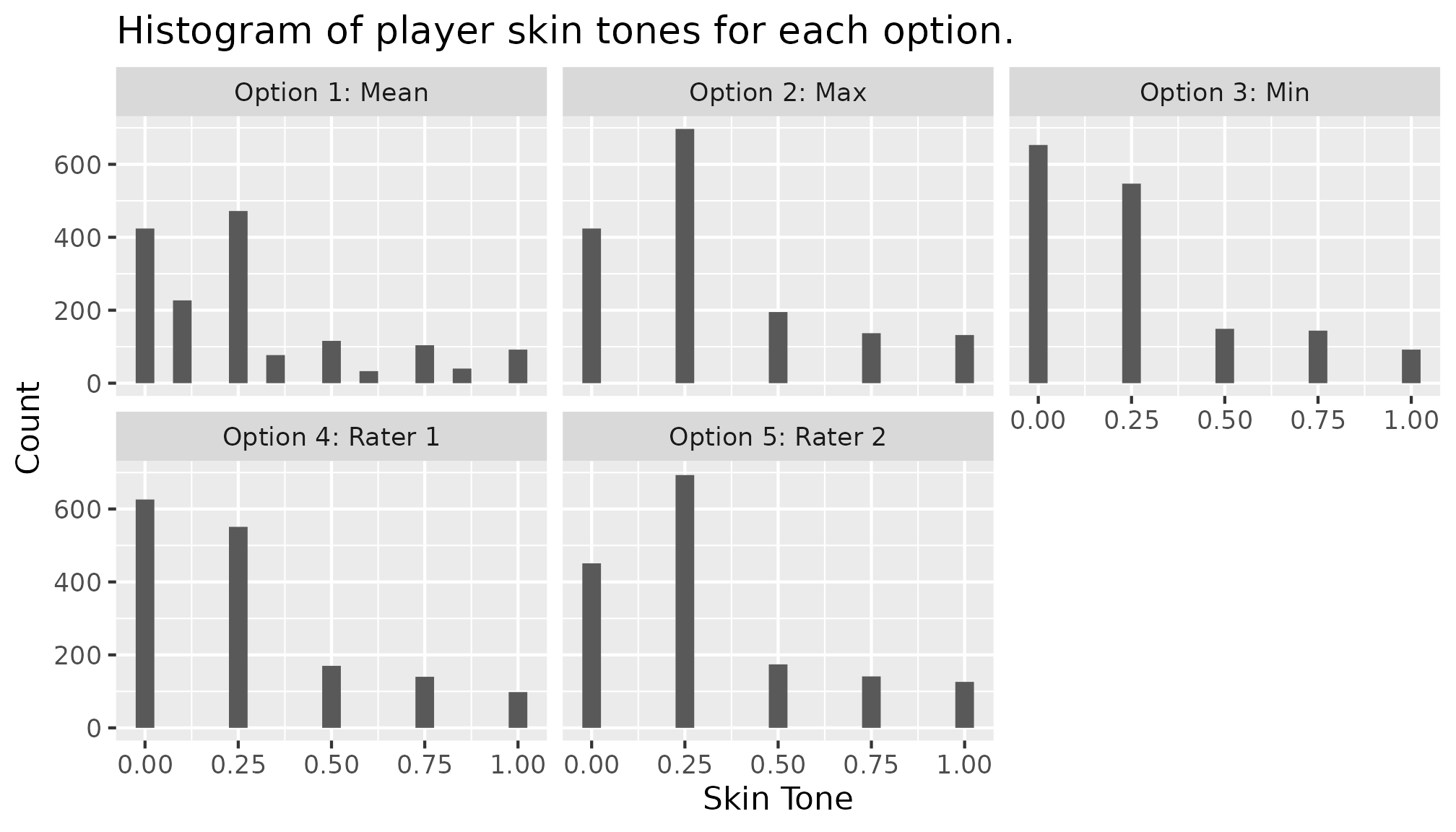
branched |>
  ggplot(mapping = aes(x = skin_tone)) +
  geom_histogram(position = "dodge", bins = 21) +
  labs(title = "Histogram of player skin tones for each option.",
       y = "Count", x = "Skin Tone") +
  facet_wrap(
    . ~ universe,
    labeller = labeller(
      universe = c(`1` = "Option 1: Mean",
                   `2` = "Option 2: Max",
                   `3` = "Option 3: Min",
                   `4` = "Option 4: Rater 1",
                   `5` = "Option 5: Rater 2")
    )
  )

References

Silberzahn, Raphael, Eric Luis Uhlmann, Dan Martin, Pasquale Anselmi, Frederik Aust, Eli C. Awtrey, Štěpán Bahník, et al. 2014. “Many Analysts, One Dataset: Making Transparent How Variations in Anlytical Choices Affect Results.” https://osf.io/gvm2z/.